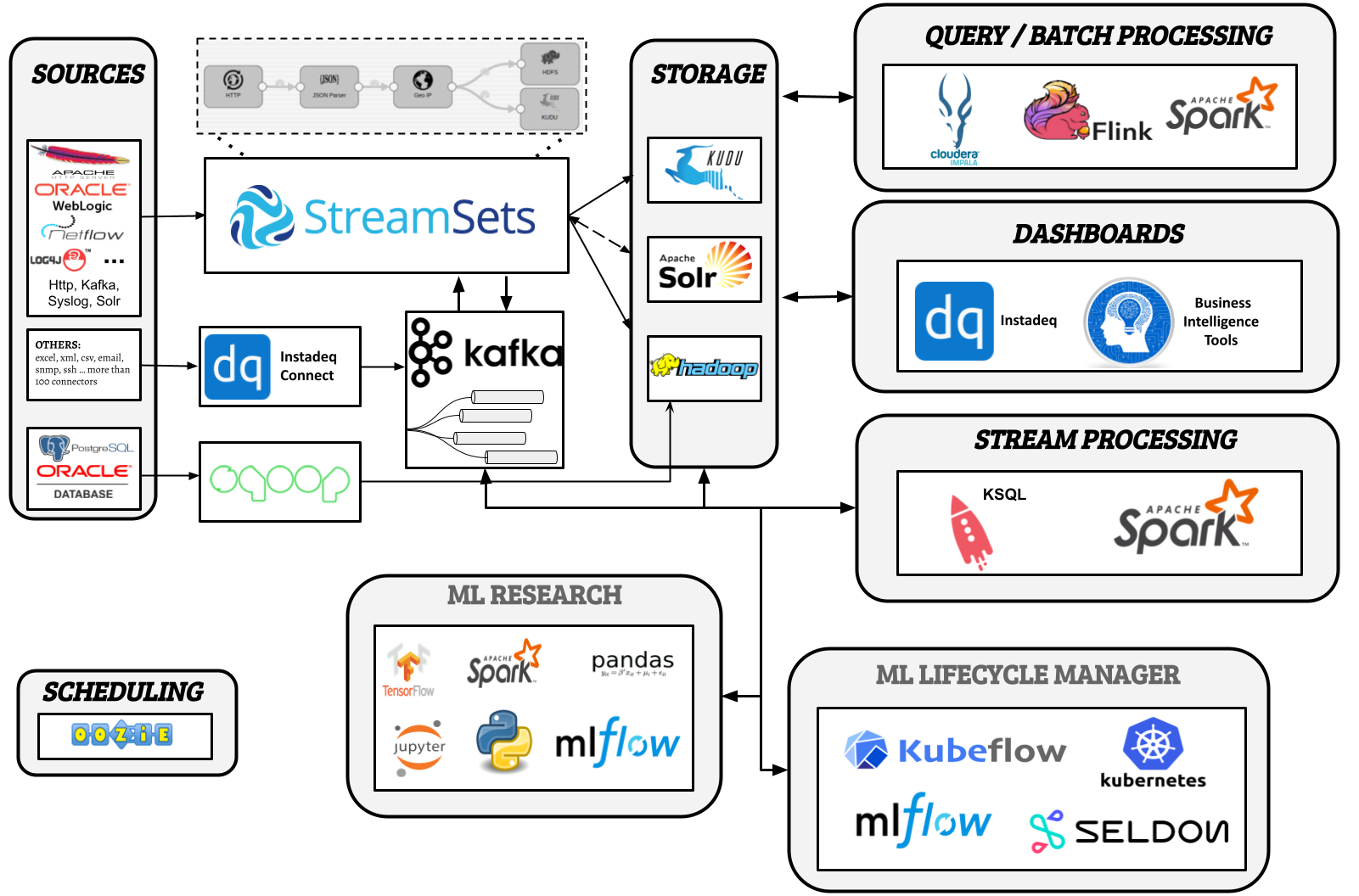
No-code History: The Geometry Theorem Machine (1959)

Geometry machine proving PARALELOGRAM EFGH
Preface
In the process of finding and sorting the history of a field one has to define a "starting point" and a set of criteria to filter what is and isn't part of the field being studied.
This series of posts is an attempt at finding both the starting point and the filter criteria, which as the series progresses hopefully will be clear enough to be shared publicly.
I find the following papers a good approximation to a starting point, the lack of a visual interface is mostly the result of technology limitations, as the papers say:
The behavior of the system would not be changed if the diagram computer were replaced by a device that could draw figures on paper and scan them.
...
Our first system does not "draw" its own initial figure, but is, instead, supplied with the diagram in the form of a list of possible coordinates for the points named in the theorem.
...
Like the human mathematician, the geometry machine makes use of the potent heuristic properties of a diagram to help it distinguish the true from the false sequences.
Note: Almost all text below are quotes from resources listed at the end with slight editions, emphasis mine, personal comments are lines starting with 💭
Introduction
In early spring, 1959, an IBM 704 computer, with the assistance of a program comprising some 20,000 individual instructions, proved its first theorem in elementary Euclidean plane geometry. Since that time, the geometry-theorem proving machine has found solutions to a large number of problems taken from high-school textbooks and final examinations in plane geometry.
Some of these problems would be considered quite difficult by the average high-school student. In fact, it is doubtful whether any but the brightest students could have produced a solution for any of the latter group when granted the same amount of prior "training" afforded the geometry machine.
The geometry machine is able to discover proofs for a significant number of interesting theorems within the domain of its ad hoc formal system (comprising theorems on parallel lines, congruence, and equality and inequality of segments and angles) without resorting to a decision algorithm or exhaustive enumeration of possible proof sequences.
Motivation
The research project which had as its consequence the geometry-theorem proving machine was motivated by the desire to learn ways to use modern high-speed digital computers for the solution of a new and difficult class of problems.
In particular, we wished to make our computer perform tasks which are generally considered to require the intervention of human intelligence and ingenuity for their successful completion.
If we restrict the universe of problems to the discovery of a proof for a theorem in some well-defined formal system, then the distinguishing characteristics of those problems of special interest to us are brought clearly into focus.
The Language
The following theorem is proved in less than a minute.
Theorem: A point on the bisector of an angle is equidistant from the sides of the angle:
Premises Angle ABD equals angle DBC Segment AD perpendicular segment AB Segment DC perpendicular segment BC Definition Right angle DAB Right angle DCB Syntactic Symmetries CA, 88, AC, DD Goals Segment AD equals segment CD
Solution:
Angle ABD equals angle DBC Premise Right angle DAB Definition of perpendicular Right angle DCB Definition of perpendicular Angle BAD equals angle BCD All right angles are equal Segment DB Assumption based on diagram Segment BD equals segment BD Identity Triangle BCD Assumption based on diagram Triangle BAD Assumption based on diagram Triangle ADB congruent triangle CDB Side-angle-angle Segment AD equals segment CD Corresponding elements of congruent triangles are equal Total elapsed time = 0.3200 minute
In less than five minutes, the machine is able to find the attached proof, which requires the construction of an auxiliary segment.
Theorem: In a quadrilateral with one pair of opposite sides equal and Parallel, the other pair of sides are equal:
Premises Quad-lateral ABCD Segment BC parallel segment AD Segment BC equals segment AD CA BA DA DB AB CB AC DC BC BD CD AD Goals Segment AB equals segment CD I am stuck, elapsed time = 0.88 minute Construct segment DB Add premise segment DB Restart problem
Solution:
Segment BC parallel segment AD Premise Opp-side CADB Assumption based on diagram Segment DB Premise Angle ADB equals angle CBD Alternate interior angles of parallel lines Segment BC equals segment AD Premise Segment BD equals segment DB Identity Triangle CDB Assumption based on diagram Triangle ABD Assumption based on diagram Triangle ABD congruent triangle CDB Side-angle-side Segment AB equals segment CD Corresponding elements of congruent triangles Total elapsed time = 4.06 minutes
How it Works
💭 The use enters the definition of a geometric shape and asks the system to prove a statement, the system will either provide the proof or inform that it's "stuck" and needs more definitions to continue. At the end the proof is provided.
Theory
Just as manipulation of numbers in arithmetic is the fundamental mode of operation in contemporary computers, manipulation of symbols in formal systems is likely to be the fundamental operating mode of the more sophisticated problem-solving computers of the future.
It seems clear that while the problems of greatest concern to lay society will be, for the most part, not completely formalizable, they will have to be expressed in some sort of formal system before they can be dealt with by machine.
Like the human mathematician, the geometry machine makes use of the potent heuristic properties of a diagram to help it distinguish the true from the false sequences.
Although the diagram is useful to the machine in other ways as well, the single heuristic "Reject as false any statement that is not valid in the diagram" is sufficient to enable the machine to prove a large class of interesting theorems, some of which contain a certain trivial kind of construction.
A heuristic is, in a very real sense, a filter that is interposed between the solution generator and the solution evaluator for a given class of problems.
The first requirement for such a filter is a consequence of the fact that its introduction into the system is never costless. It must, therefore, be sufficiently "nonporous" to result in a net gain in problem-solving efficiency.
Secondly, a heuristic will generally remove from consideration a certain number of sequences that are quick and elegant solutions, if not indeed all solutions, to some potential problems within the domain of the problem-solving machine.
The filter must, then, be carefully matched to that subclass of problems in the domain containing those that are considered "interesting," and are therefore likely to be posed to the machine.
The decisive point in favor of geometry was the great heuristic value of the diagram. The creative scientist generally finds his most valuable insights into a problem by considering a model of the formal system in which the problem is couched. In the case of Euclidean geometry, the semantic interpretation is so useful that virtually no one would attempt the proof of a theorem in that system without first drawing a diagram; if not physically, then in the mind's eye.
Trivia
The geometry machine is in reality a particular state configuration of the IBM 704 electronic Data Processing Machine.
In order to ease the task of writing so massive and complex a machine code, a convenient special-purpose list processing language was designed to be compiled by the already available FORTRAN system for the IBM 704 computer. The authors feel that had they not made free use of an intermediate programming language, it is likely that the geometry program could not have been completed.
💭 The language mentioned is a precursor of LISP called Information Processing Language (1956)