Statecharts: A Visual Formalism For Complex Systems

This is a summary of the paper: Statecharts: A Visual Formalism For Complex Systems

statecharts = state-diagrams + orthogonality + depth + broadcast-communication

Summary

A broad extension of the conventional formalism of state machines and state diagrams, that is relevant to the specification and design of complex discrete-event systems, such as multi-computer real-time systems, communication protocols and digital control units. Our diagrams, which we call statecharts, extend conventional state-transition diagrams with essentially three elements, dealing, respectively, with the notions of hierarchy, concurrency and communication.

Statecharts are thus compact and expressive, small diagrams can express complex behavior, as well as compositional and modular.

Statecharts enable viewing the description at different levels of detail, and make even very large specifications manageable and comprehensible.

Statecharts counter many of the objections raised against conventional state diagrams, and thus appear to render specification by diagrams an attractive and plausible approach.

Statecharts constitute a visual formalism for describing states and transitions in a modular fashion, enabling clustering, orthogonality (i.e., concurrency) and refinement, and encouraging ‘zoom' capabilities for moving easily back and forth between levels of abstraction.

The kernel of the approach is the extension of conventional state diagrams by AND/OR decomposition of states together with inter-level transitions, and a broadcast mechanism for communication between concurrent components.

The graphics is actually based on a more general concept, the higraph, which combines notions from Euler circles, Venn diagrams and hypergraphs, and which seems to have a wide variety of applications.

An arrow will be labelled with an event (or an abbreviation of one) and optionally also with a parenthesized condition, Mealy-like outputs, or actions.

Problem

The literature on software and systems engineering is almost unanimous in recognizing the existence of a major problem in the specification and design of large and complex reactive systems.

The problem is rooted in the difficulty of describing reactive behavior in ways that are clear and realistic, and at the same time formal and rigorous, sufficiently so to be amenable to detailed computerized simulation. The behavior of a reactive system is really the set of allowed sequences of input and output events, conditions, and actions, perhaps with some additional information such as timing constraints.

Reactive Systems

A reactive system, in contrast with a transformational system, is characterized by being, to a large extent, event-driven, continuously having to react to external and internal stimuli.

Representation

Much of the literature also seems to be in agreement that states and events are a piori a rather natural medium for describing the dynamic behavior of a complex system.

A basic fragment of such a description is a state transition, which takes the general form “when event E occurs in state A, if condition C is true at the time, the system transfers to state B”

State diagrams are simply directed graphs, with nodes denoting states, and arrows (labelled with the triggering events and guarding conditions) denoting transitions.

Requirements

A good state/event approach should also cater naturally for more general and flexible statements, such as

• (1) “in all airborne states, when yellow handle is pulled seat will be ejected”,

• (2) “gearbox change of state is independent of braking system”,

• (3) “when selection button is pressed enter selected mode”,

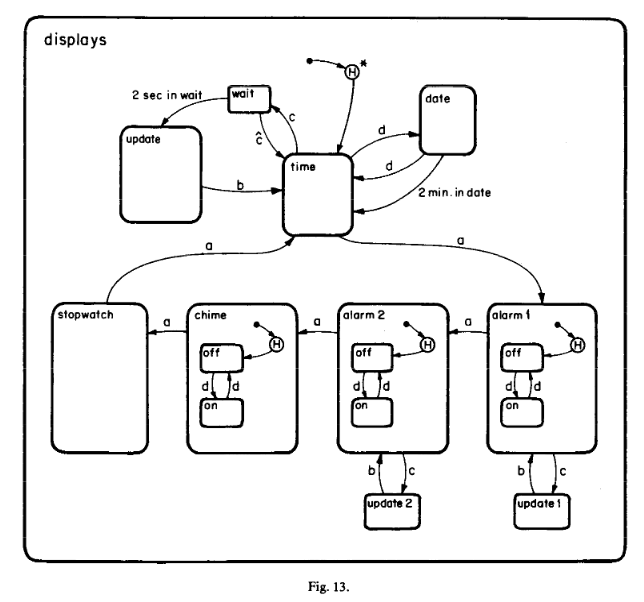
• (4) “display-mode consists of time-display, date-display and stopwatch-display”.

Proposed Solutions

Clause (1) calls for the ability to cluster states into a superstate

(2) Introduces independence, or orthogonality

(3) Hints at the need for more general transitions than the single event-labelled arrow

(4) Captures the refinement of states.

Solutions

State-levels: Clustering and refinement

Clustering states inside other states via exclusive-or (XOR) semantics

The outer state is an abstraction of the inner states

Enables Zoom in/out

A default state can be specified, analogous to start states of finite state automata

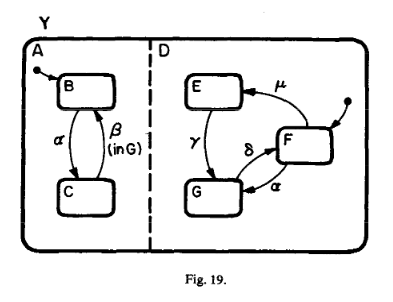
Orthogonality: Independence and concurrency

Being in a state, the system must be in all of its AND components

The notation is the physical splitting of a box into components using dashed lines

The outer (AND) state is the orthogonal product of the inner states

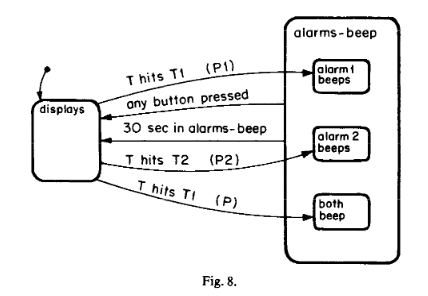
Synchronization: a single event causes two simultaneous happenings

Independence: a transition is the same whether the system is in any given inner state

Orthogonality avoids exponential blow-up in the number of states, usual in classical finite-state automata or state diagrams

Formally, orthogonal product is a generalization of the usual product of automata, the difference being that the latter is usually required to be a disjoint product, whereas here some dependence between components can be introduced, by common events or "in G"-like conditions.

Condition and selection entrances

Conditional entrance to an inner state according to guards (like an if/else statement)

Selection occurs when the state to be entered i determined in a simple one-one fashion by the value of a generic event (like a switch statement)

Delays and timeouts

The expression timeout(event, number) represents the event that occurs precisely when the specified number of time units have elapsed from the occurrence of the specified events.

Unclustering

Laying out parts of the statechart not within but outside of their natural neighborhood.

This conventional notation for hierarchical description has the advantage of keeping the neighborhood small yet the parts of interest large.

Taking this to the extreme yields and/or trees, undermining the basic area-dominated graphical philosophy. However, adopting the idea sparingly can be desirable.

Actions and Activities

What 'pure' statecharts represent is the control part of the system, which is responsible for making the time-independent decisions that influence the system's entire behavior.

What is missing is the ability of statecharts to generate events and to change the value of conditions.

These can be expressed with the action notation that can be attached to the label of a transition.

Actions are split-second happenings, instantaneous occurrences that take ideally zero time.

Activities are durable, they take some time, whereas actions are instantaneous. In order to enable statecharts to control activities too, it needs two special actions to start and stop activities. start(X) and stop(X)

Possible extensions to the formalism

Parameterized states

Different states have identical internal structure. Some of the most common ones are those situations that are best viewed as a single state with a parameter.

Overlapping states

Statechart don't need to be entirely tree-like.

Overlapping states act as OR, they can be used economically to describe a variety of synchronization primitives, and to reflect many natural situations in complex systems. Note that they cause semantical problems, especially when the overlapping involves orthogonal components.

Incorporating temporal logic

It is possible to specify ahead of time many kinds of global constraints in temporal logic, such as eventualities, absence from deadlock, and timing constraints.

Then attempt to verify that the statechart-based description satisfies the temporal logic clauses.

Recursive and probabilistic statecharts

Recursion can be done by specifying the name of a separate statechart.

Probabilistic statecharts can be done by allowing nondeterminism.

Practical experience and implementation

The statechart formalism was conceived and developed while the author was consulting for the Israel Aircraft Industries on the development of a complex state-of-the-art avionics system for an advanced airplane.

This projects can demand bewildering levels of competence from many people of diverse backgrounds.

Thee people have to continuously discuss, specify, design, construct and modify parts of the system.

The languages and tools they use in doing their work, and for communicating
ideas and decisions to others, has an effect on the quality, maintainability
and expedition of the system that cannot be overestimated.